Machine Learning in Algo Trading: Linear Regression in MQL4

Machine learning is increasingly shaping the landscape of algorithmic trading by allowing traders to analyse large amounts of data, uncover hidden patterns, and make more data-driven predictions. By leveraging machine learning models, trading strategies can be optimised for better accuracy and adaptability. This article explores the types of machine learning used in algorithmic trading, their applications, and provides a practical example of implementing linear regression directly within MQL4 to forecast price trends.

Types of Machine Learning in Algorithmic Trading

Machine learning (ML) encompasses a variety of techniques that enable systems to learn from data. In algorithmic trading, ML models are primarily used to detect patterns, make predictions, and adapt to changing market conditions. The main types of ML approaches used in trading include:

1. Supervised Learning:

How it Works: Supervised learning algorithms train on labelled datasets, where each input has a known output. This allows the model to learn relationships and make predictions on new data.
Applications:
- Price Prediction: Predicting future asset prices or price directions.
- Classification: Categorising market conditions as bullish, bearish, or neutral to guide trading decisions.
Examples: Linear regression, decision trees, and support vector machines (SVM).

2. Unsupervised Learning:

How it Works: Unsupervised learning algorithms work on unlabelled data, identifying patterns or clusters within the dataset without predefined labels.
Applications:
- Market Clustering: Identifying unique market conditions by grouping data points with similar characteristics.
- Anomaly Detection: Detecting unusual market events or patterns that may signal volatility or reversals.
Examples: K-means clustering and principal component analysis (PCA).

3. Reinforcement Learning (RL):

How it Works: Reinforcement learning involves training an agent to make decisions through trial and error, receiving rewards or penalties based on its actions. Over time, the agent optimises its strategy to maximise cumulative rewards.
Applications:
- Adaptive Trading: Developing adaptive trading strategies that respond dynamically to changing market conditions.
- Optimal Execution: Optimising order execution by learning from historical order book data.
Examples: Q-learning and deep Q-networks (DQN).

Each type of ML approach has its unique strengths, and selecting the right model depends on the trading objective and data characteristics.

Popular Machine Learning Models for Trading

1. Linear Regression:

Type: Supervised learning.
Purpose: Forecast price trends by modelling linear relationships between price and time.
Example Use: Predicting future price movements based on past trends.

2. Decision Trees and Random Forests:

Type: Supervised learning.
Purpose: Make decisions by learning if-then rules from data, often used to categorise market conditions.
Example Use: Classifying price movements as buy, hold, or sell.

3. K-Means Clustering:

Type: Unsupervised learning.
Purpose: Segment data into clusters, useful for identifying different market regimes or conditions.
Example Use: Grouping assets with similar behaviours or identifying unique market phases.

4. Neural Networks:

Type: Supervised and unsupervised learning.
Purpose: Model complex relationships in large datasets, useful for time-series prediction and sentiment analysis.
Example Use: Forecasting price based on historical patterns and news sentiment.

5. Reinforcement Learning:

Type: Reinforcement learning.
Purpose: Adapt to changing markets by learning from interactions, ideal for high-frequency trading and optimal execution.
Example Use: Dynamic portfolio rebalancing.

Implementing Linear Regression in Algorithmic Trading

To demonstrate machine learning in MQL4, we’ll implement Linear Regression, a supervised learning technique commonly used in trading to identify trends and forecast price directions. Linear regression is ideal for algorithmic trading due to its simplicity and ability to model the relationship between price and time directly within MQL4.

Linear Regression Formula:

Where:

a is the intercept, the point where the line crosses the y-axis.
b is the slope, representing the rate of change in price over time.

The slope and intercept provide a linear approximation of price trends, which we can use to forecast future prices based on recent data.

Calculating Linear Regression in MQL4

To calculate the slope ( $b$ ) and intercept ( $a$ ) for a set of data points (e.g., closing prices of the last 20 bars), we use the least squares regression formulas:

1. Slope (b):

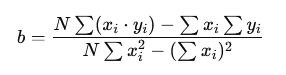
Slope (b)

2. Intercept (a):

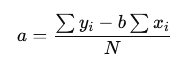
Intercept (a)

Where:

$N$ is the number of data points (bars),
$x_{i}$ represents each time increment (e.g., bar index),
$y_{i}$ represents the closing price.

Linear Regression Example in MQL4

The following MQL4 code demonstrates how to implement a linear regression model to forecast price trends based on the slope and intercept calculated from historical data.

// Linear Regression Trading Strategy in MQL4
input int Period = 20;                // Number of bars for regression calculation
input double LotSize = 0.1;           // Lot size for orders
 
// Global variables to track trade status
bool buyTradeOpen = false;
bool sellTradeOpen = false;
 
void OnTick() {
   double slope, intercept;
   CalculateLinearRegression(slope, intercept);
 
   // Forecast the price for the next bar
   double forecast = intercept + slope * Period;
   double currentPrice = iClose(NULL, 0, 0);
 
   // Buy if forecasted price is above current price
   if (forecast &gt; currentPrice &amp;&amp; !buyTradeOpen) {
       if (sellTradeOpen) CloseSell();
       OpenBuy();
   }
   // Sell if forecasted price is below current price
   else if (forecast &lt; currentPrice &amp;&amp; !sellTradeOpen) {
       if (buyTradeOpen) CloseBuy();
       OpenSell();
   }
}
 
// Function to calculate linear regression slope and intercept
void CalculateLinearRegression(double &amp;slope, double &amp;intercept) {
   double sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;
   int N = Period;
 
   for (int i = 0; i &lt; N; i++) { double x = i; // Time variable (index of bar) double y = iClose(NULL, 0, i); // Closing price sumX += x; sumY += y; sumXY += x * y; sumX2 += x * x; } // Calculate slope (b) and intercept (a) slope = (N * sumXY - sumX * sumY) / (N * sumX2 - sumX * sumX); intercept = (sumY - slope * sumX) / N; } // Function to open a buy position void OpenBuy() { int ticket = OrderSend(Symbol(), OP_BUY, LotSize, Ask, 3, 0, 0, "Linear Regression Buy", 0, 0, clrGreen); if (ticket &gt; 0) {
       buyTradeOpen = true;
       sellTradeOpen = false;
       Print("Buy order opened based on linear regression forecast.");
   } else {
       Print("Error opening buy order: ", GetLastError());
   }
}
 
// Function to open a sell position
void OpenSell() {
   int ticket = OrderSend(Symbol(), OP_SELL, LotSize, Bid, 3, 0, 0, "Linear Regression Sell", 0, 0, clrRed);
   if (ticket &gt; 0) {
       sellTradeOpen = true;
       buyTradeOpen = false;
       Print("Sell order opened based on linear regression forecast.");
   } else {
       Print("Error opening sell order: ", GetLastError());
   }
}
 
// Function to close any open buy position
void CloseBuy() {
   for (int i = OrdersTotal() - 1; i &gt;= 0; i--) {
       if (OrderSelect(i, SELECT_BY_POS) &amp;&amp; OrderType() == OP_BUY) {
           OrderClose(OrderTicket(), OrderLots(), Bid, 3, clrGreen);
           buyTradeOpen = false;
           Print("Buy order closed.");
       }
   }
}
 
// Function to close any open sell position
void CloseSell() {
   for (int i = OrdersTotal() - 1; i &gt;= 0; i--) {
       if (OrderSelect(i, SELECT_BY_POS) &amp;&amp; OrderType() == OP_SELL) {
           OrderClose(OrderTicket(), OrderLots(), Ask, 3, clrRed);
           sellTradeOpen = false;
           Print("Sell order closed.");
       }
   }
}

// Linear Regression Trading Strategy in MQL4 input int Period = 20; // Number of bars for regression calculation input double LotSize = 0.1; // Lot size for orders // Global variables to track trade status bool buyTradeOpen = false; bool sellTradeOpen = false; void OnTick() { double slope, intercept; CalculateLinearRegression(slope, intercept); // Forecast the price for the next bar double forecast = intercept + slope * Period; double currentPrice = iClose(NULL, 0, 0); // Buy if forecasted price is above current price if (forecast > currentPrice && !buyTradeOpen) { if (sellTradeOpen) CloseSell(); OpenBuy(); } // Sell if forecasted price is below current price else if (forecast < currentPrice && !sellTradeOpen) { if (buyTradeOpen) CloseBuy(); OpenSell(); } } // Function to calculate linear regression slope and intercept void CalculateLinearRegression(double &slope, double &intercept) { double sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0; int N = Period; for (int i = 0; i < N; i++) { double x = i; // Time variable (index of bar) double y = iClose(NULL, 0, i); // Closing price sumX += x; sumY += y; sumXY += x * y; sumX2 += x * x; } // Calculate slope (b) and intercept (a) slope = (N * sumXY - sumX * sumY) / (N * sumX2 - sumX * sumX); intercept = (sumY - slope * sumX) / N; } // Function to open a buy position void OpenBuy() { int ticket = OrderSend(Symbol(), OP_BUY, LotSize, Ask, 3, 0, 0, "Linear Regression Buy", 0, 0, clrGreen); if (ticket > 0) { buyTradeOpen = true; sellTradeOpen = false; Print("Buy order opened based on linear regression forecast."); } else { Print("Error opening buy order: ", GetLastError()); } } // Function to open a sell position void OpenSell() { int ticket = OrderSend(Symbol(), OP_SELL, LotSize, Bid, 3, 0, 0, "Linear Regression Sell", 0, 0, clrRed); if (ticket > 0) { sellTradeOpen = true; buyTradeOpen = false; Print("Sell order opened based on linear regression forecast."); } else { Print("Error opening sell order: ", GetLastError()); } } // Function to close any open buy position void CloseBuy() { for (int i = OrdersTotal() - 1; i >= 0; i--) { if (OrderSelect(i, SELECT_BY_POS) && OrderType() == OP_BUY) { OrderClose(OrderTicket(), OrderLots(), Bid, 3, clrGreen); buyTradeOpen = false; Print("Buy order closed."); } } } // Function to close any open sell position void CloseSell() { for (int i = OrdersTotal() - 1; i >= 0; i--) { if (OrderSelect(i, SELECT_BY_POS) && OrderType() == OP_SELL) { OrderClose(OrderTicket(), OrderLots(), Ask, 3, clrRed); sellTradeOpen = false; Print("Sell order closed."); } } }

Explanation of the Linear Regression Strategy

1. Parameters:

Period: The number of bars (time increments) used for calculating the regression line.
LotSize: The trade size for each order.

2. Trade Execution:

The CalculateLinearRegression() function computes the slope and intercept of the linear regression line based on the closing prices of the last Period bars.
The algorithm then forecasts the price for the next time step. If the forecasted price is higher than the current price, a buy order is triggered. Conversely, if the forecasted price is lower, a sell order is initiated.

3. Functions:

CalculateLinearRegression(): Calculates the slope and intercept for the linear regression line, enabling the prediction of future price trends.
OpenBuy() and OpenSell(): Place buy and sell orders based on the trend direction predicted by the linear regression model.
CloseBuy() and CloseSell(): Close existing trades when a new, opposing signal is generated.

This strategy offers a simple yet effective way to leverage linear regression in forecasting and trading based on recent trends.

Optimising Linear Regression in Algorithmic Trading

1. Adjust the Period Parameter:

Experiment with different values for the Period to balance sensitivity and stability. Shorter periods may capture short-term trends but can be more volatile, while longer periods offer smoother trends but may react slowly to market changes.

2. Combine with Other Indicators:

Use linear regression in conjunction with other indicators, such as RSI or MACD, to add an extra layer of confirmation, reducing the risk of false signals.

3. Backtest and Monitor Performance:

Regularly backtest the strategy across various market conditions to ensure it performs consistently. Monitoring live performance helps you identify when adjustments are necessary.

4. Account for Market Volatility:

In highly volatile markets, linear regression predictions may be less reliable. Consider adjusting trade sizes or using a volatility filter to improve accuracy during turbulent times.

Conclusion

Linear regression is a straightforward yet powerful tool in algorithmic trading, providing a foundation for predicting price trends. By implementing linear regression directly within MQL4, traders can leverage a machine learning-based approach to forecast and act on price movements. This example demonstrates how machine learning concepts, such as linear regression, can be practically applied in MQL4 without the need for complex external tools, making it accessible to a wide range of algorithmic traders.

In the next article, we’ll explore High-Frequency Trading (HFT) Strategies and Challenges, diving into the mechanics and requirements for building high-frequency trading algorithms.